On April 9, 1963, Winston Churchill Was Made An Honorary Citizen Of The United States By John F. Kennedy.

Are Complex Numbers Really Numbers?

If you look through definitions of “number” most will say that numbers are used to represent quantities (amounts or measures). Whole numbers 0, 1, 2, 3, … are probably the first numbers that come to mind and they are often used to count things like say how may watermelons jimmy has. But when quantifying things like money, whole numbers are not always enough and so we have rational numbers (which include the whole numbers but also fractions and numbers with finite or repeating decimal expansions). Yet, sometimes even these numbers are not enough to express certain quantities. Pi, for example, is not a rational number but is certainly a number as it represents the quantity that is the ratio of a circle’s circumference to its diameter. It can be shown that the number pi has an infinite decimal expansion with no repeating patterns, and so a number like pi is called an irrational number. (Because they are silly? Although at first some thought so, the term irrational just means not rational.)  More specifically, pi is a transcendental number as it is not the root of any polynomial. (Transcendental, because they transcend the usual notion of number? Idk. Again, strange names.) So, the rational numbers were extended to the real numbers to include both rational and irrational numbers. Either way, we see that both rational and irrational numbers are truly numbers since they can be used to represent quantities.

What about complex numbers though? Are they really numbers, or do people just call them “numbers”? So, we should ask, can complex numbers represent some amount or measure of something? Can jimmy have i watermelons? No, but jimmy can’t really have pi watermelons either and pi is a number. Jimmy may have a watermelon that weighs pi pounds though (the only way to know this would be if jimmy had a scale with infinite accuracy, which, turns out, he does). Okay but can jimmy have a watermelon weighing i pounds? That doesn’t seem to make sense. To see if complex numbers can represent quantities we need to elaborate on what complex numbers are exactly.

The complex numbers are the real numbers extended to include the square root of negative 1 (i) and all its multiples. They have the form a+bi where a and b are real numbers. i is called an imaginary number (named imaginary because, i is not a real number, but this implies numbers like i are somehow not “real”, in the usual English sense of the word (are any numbers really “real”?) again, with the names). What truly makes complex numbers different than the other numbers we have discussed is that they “live” in 2 dimensions (the complex plane); complex numbers (e.g., 7+2i) have a real part (7) and an imaginary part (2i). While real numbers (which include whole, rational, and irrational numbers) “live” in one dimension (they can be found anywhere on the number line).

So, a complex number is a sort of two-dimensional quantity, it has a real measure and an imaginary measure. This makes them strange as numbers. We know 12 is bigger than 11 and that there are a bunch of numbers in-between 11 and 12, but which is bigger 2-8i or 3+i? Complex numbers cannot be compared in the same way i.e., there is no way to order complex numbers from smallest to largest.

These properties make complex numbers more abstract than typical numbers we encounter day to day. Nevertheless, “complex numbers are useful abstract quantities that can be used in calculations and result in physically meaningful solutions. However, recognition of this fact is one that took a long time for mathematicians to accept.”—Wolfram MathWorld http://mathworld.wolfram.com/ComplexNumber.html

Too much sex causes genitals to change shape, beetle study shows

Sexual conflict between males and females can lead to changes in the shape of their genitals, according to research on burying beetles by scientists at the University of Exeter.

The study, published in the journal Evolution, provides new evidence that conflict over how often mating takes place can lead to males evolving longer penis-like organs and females larger ‘claws’ on their genitalia, within ten generations.

“Our research demonstrates the general importance of conflicts of interest between males and females in helping to generate some of the biodiversity that we see in the natural world. It’s fascinating how genital evolution can happen so fast – in ten generations – showing how rapidly evolutionary changes can occur.”

Paul E. Hopwood, Megan L. Head, Eleanor J. Jordan, Mauricio J. Carter, Emma Davey, Allen J. Moore, Nick J. Royle. Selection on an antagonistic behavioral trait can drive rapid genital coevolution in the burying beetle,Nicrophorus vespilloides. Evolution, 2016; DOI: 10.1111/evo.12938

Science Fact Friday: Tetrodotoxin, ft. a small gif because I’m avoiding my real obligations. Why does tetrodotoxin not affect its host? More studies need to be done but at least a few species possess mutated sodium ion channels. The tetrodotoxin can’t interact efficiently with the altered channels.

Another interesting tidbit: Animals with tetrodotoxin can lose their toxicity in captivity. It is suspected that the animals accumulate the toxic bacteria as a side-effect of their diet. After several years of captivity on a tetrodotoxin-bacteria-free diet, the bacterial colonies living in the animals die, residual toxin is cleared from the system, and the animal is safe to handle.

David in Singapore, Serious Moonlight Tour 1983

Photo © Denis O’Regan

It’s easy:  Form a triangle, then a hexagon, then a bicycle wheel

This is the general mechanism on how a spider spins its web (talk about engineering, right?). When an insect gets caught in its web, the vibrations caused by the insect is felt by the spider which then rushes to engulf its prey.

Now here is the trippy part ; This is the effect of drugs on the pattern of the web.

Hope you are having a great week. Have a good one!

* Spider spinning a web (video) (if you find a better full video let us know)

** Spiders on drugs -  NASA article ; Video

12 Amazing Facts About Elephants

In honor of World Elephant Day, we present you with 12 little known facts about one of our favorite creatures…in GIFs, of course.

1. Elephants know every member of their herd and are able to recognize up to 30 companions by sight or smell. 

2. They can remember and distinguish particular cues that signal danger and can recall locations long after their last visit.

3. An elephant’s memory is not limited to its herd, nor is it limited to its species. In one instance, two circus elephants that performed together rejoiced when crossing paths 23 years later. Elephants have also recognized humans that they once bonded with after decades apart. 4. 

4. The elephant boasts the largest brain of any land mammal as well as an impressive encephalization quotient (the size of the animal’s brain relative to its body size). The elephant’s EQ is nearly as high as a chimpanzee’s.

5. The elephant brain is remarkably similar to the human brain, with as many neurons and synapses, as well as a highly developed hippocampus and cerebral cortex.

6. Elephants are one of the few non-human animals to suffer from post-traumatic stress disorder.

7. Elephants are creative problem solvers. 

8. Don’t try to outsmart an elephant! They have an understanding of basic arithmetic and can even keep track of relative quantities.

9. Elephants communicate using everything from body signals to infrared rumbles that can be heard from kilometers away. Their understanding of syntax suggests that they have their own language and grammar. 

10. Elephants can recognize 12 distinct tones of music and recreate melodies.

11. Elephants are the only non-human animals to mourn their dead, performing burial rituals and returning to visit graves. 

12. Elephants are one of the few species who can recognize themselves in the mirror.

Given what we now know about elephants, and what they continue to teach us about animal intelligence, it is more important than ever to make sure that these magnificent creatures do not vanish.

Check out some more fun elephant facts here and be sure to watch the TED-Ed Lesson Why elephants never forget - Alex Gendler

Animation by the ever-talented Avi Ofer

Harmonograph, H. Irwine Whitty, 1893

“The facts that musical notes are due to regular air-pulses, and that the pitch of the note depends on the frequency with which these pulses succeed each other, are too well known to require any extended notice. But although these phenomena and their laws have been known for a very long time, Chladni, late in the last century, was the first who discovered that there was a connection between sound and form.”

source here

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

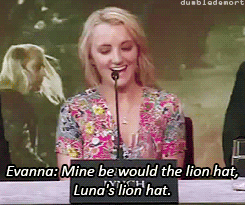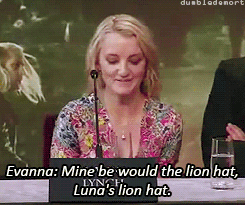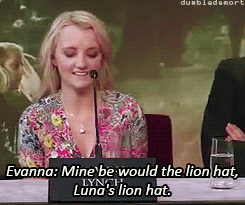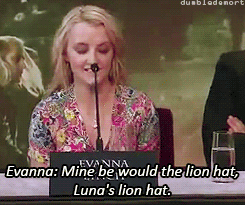
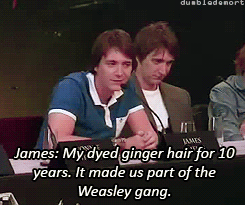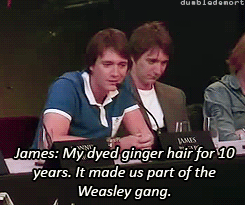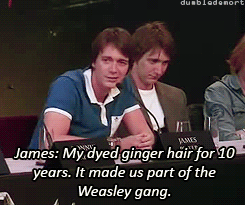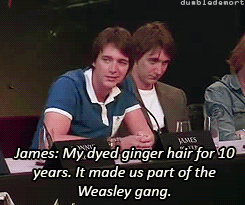
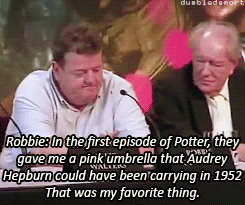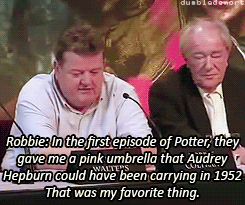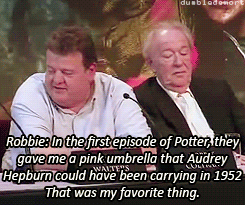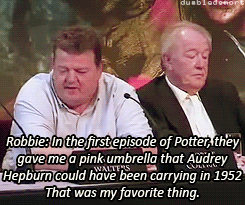
What was your favorite prop or costume from the “Harry Potter” films?

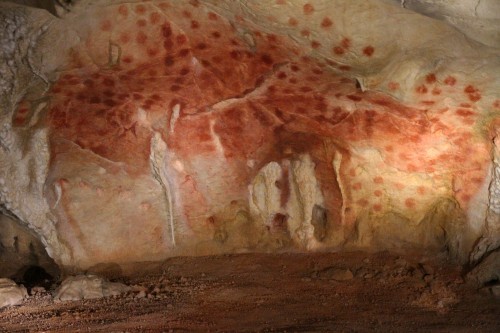
CHAUVET CAVE: 

THE  Chauvet Cave (also known as the Chauvet-Pont-d’Arc Cave) is a Palaeolithic cave situated near Vallon-Pont-d’Arc in the Ardèche region of southern France that houses impeccably preserved, exquisite examples of prehistoric art. 

Now reliably dated to between c. 33,000 and c. 30,000 years ago, the numerous and diverse animals that dot the interior walls of the cave – both painted and engraved – show such high artistic quality that they were initially thought to have been closer in age to the similarly stunning, but much younger art in caves such as the Lascaux Cave. Its age and artistry have made us reconsider the story of art as well as the capabilities of these humans. The cave has been granted UNESCO World Heritage status.

Read More 

Article by Emma Groeneveld on AHE